Introduction

Graph netowrks have got a lot of attention in the past decade. Almost every type of data can be represented as a graph. In that sense, newtwork analysis can be a powerfull and usesuful approach as an exloratory data analysis approach to graph neural networks (GNN). This post will focus on Network Analysis of a real data network presented by (Valentin et al., 2024). In the next section, I will make a brief introduction about the dataset and the context on which it was produced before we dive into the graph analysis part

Disease outbreak

In the domain of epidemiology, an outbreak is defined as a sudden increase in the disease frequency, related to time, place, and observed population (Reintjes and Zanuzdana, 2009) Deasease outbreaks are usually reported by agencies that are spread around the globe. Thus, these agencies play a key role to minimize effects of any epidemics, , since if outbreak events are reported early, govermantal organizations may act in time to avoid the rapid spread rate of a possible infectious deasese.An agency must declares and event when an alert is triggered and confirmed by local authorities. So the presence of agencies in all geographical levels (local, regional and global) is essential to stop an eventual epidemic. In veterinary epidemiology, the suveillance of this events is more complex, since animal farms are usually on remote areas and latelly reported by certain type of agencies, but not by others.

Thus, the use of graph network visualization tool could give us some insights about why and how agencies declare a certain type of event and how the declaration of events are connected.

The dataset

The official dataset can be found here. This dataset contains sveral csv files, but will focus on 3 main files :

• The sources.csv : represents the data about the source of outbreak declaration,
• The event.csv : represents the data about each outbreak event,
• The event_source.csv : represents all outbreak declared events

If we transform our data into a graph, source and event will be considered as node types, and event_source are edges of our graph. But before transforming the dataset into a graph, it is good to know which type the of graph we are working with

Graph types

In graph theory, graphs can be classed by different ways (e.g. interconnectivity, number of edges, etc). An exaustive list (with a visual representation) with several types of graphs can be found here. In our case, every source of outbreak declares (edge) many events. With means that for every source of outbreak, there is at least one event associated to the that source. And one event can be associated to many sources. This type of graph is call a bipartite graph :

Examples of bipartite graphs
Source https://mathworld.wolfram.com/BipartiteGraph.html

Bipartite graphs are considered to be complete (or biclique) when every graph vertex of the first set is connected to every vertex of the second set. This is not our case, since not every source declares all events

Buiding the graph with Networkx

Networkx is a python library for network analysis, aloow creation, manipulation and many other features when working with simple and complex network. In order to create a graph using Networkx, we must map the the source dataframe into a tuple. Given the formal bipartite graph definition :

where \(U\) and \(V\) represent bi parts (nodes) of the graph, and \(E\) denoting the edges of graph. In that sense, must first build some mapping to feed the graph creation using Networkx. This is done separetelly for each node : the mappings are just list of tuples (for each type of node), where each node can contain features, represented by a dictionary of attribute name and value. For the nodes (source and event) creation, the code is the same :

source_nodes_mappings = [(s,{"type_source":ts}) for s, ts in zip(list(source['source']),list(source['type_source']))]
event_nodes_mappings = [(e,{"region":r}) for e, r in zip(list(events['id_event']),list(events['region']))]

and the output with the top four nodes of event would be :

[(323, {'region': 'EUR'}), (309, {'region': 'EUR'}), (353, {'region': 'EUR'}), (325, {'region': 'EUR'})]

Notice that for each node, we added a dictionary containing the attribute name and its value. We could as many as we want. But for the sake of simplicity, we added the type of source (for source nodes) and region (for event nodes). And it’s done for nodes.

To build the edges, we must build a triplet containing \((S,T,E)\) where \(S\) is the source node (in our case, the source dataframe), \(T\) for target node (event dataframe) and \(E\) for every edge, represented by the event_source data frame. Since the edges are all maped in the event_source dataframe, we can proceed applying the following code :

source_event_mapping_list = [(s,e,{"num":n}) for s, e, n in zip(list(events_source_early['source']),
                                                                list(events_source_early['id_event']),
                                                                list(events_source_early['n']))]

and the output with the top four edges of edges would be :

[('Channel NewsAsia', 293, {'num': 1}), ('DesMoinesRegister.com', 293, {'num': 1}),
('Devdiscourse', 293, {'num': 2}), ('Free Malaysia Today', 293, {'num': 1})]

As for nodes, we also decided to add the only one attribute (n) of each edge in the graph. Finally, we use the defined mapings to initialize a network using networkx :

import networkx as nx

# Initialize the graph
G = nx.Graph()

# Add nodes with the node attribute "bipartite"
G.add_nodes_from(source_nodes, bipartite="Source Type",color="blue" )
G.add_nodes_from(event_nodes, bipartite="Region", color="red")

# Add edges only between nodes of opposite node sets
G.add_edges_from(source_event_mapping_list)

print(list(Ge.nodes)[:10])
print(list(Ge.edges)[:4])

The output :

['OIE', 'Malaysia Vet Auth', 'Gulf Business News', 'Vietnam Vet Auth', 'Reuters', 'The Star Online', 
'Sabbah Vet Auth', 'Devdiscourse', 'Deccan Chronicle', 'The Borneo Post']
[('OIE', 293), ('OIE', 294), ('OIE', 295), ('OIE', 296)]

NetworkX will use the exacly names of nodes and edges as it is in when we output the network. In our case, we want source nodes to be named by type_source and event nodes to be named by region. So we must relabel them

Relabel nodes and edges

To relabel nodes and edges, we will use the relabel function provided by Networkx. To apply the function, we must provide the Graph we want to change and a mapping (as a list of tuples) containg the old and the new name of nodes and edges. In our case, we already have a list containing the type of sources : source_nodes_mappings. To create our mapping we do:

# Crete source mapping from a list
mapping_source_to_type_source = dict([(source[0], source[1].get("type_source")) for source in source_nodes_mappings])

# Relabel source nodes
G = nx.relabel_nodes(Gai, mapping_source_to_type_source_ai)

# Show graph nodes after relabel
print(G.nodes[:15])

which gives us now the nodes by type of source :

['int. org.', 'vet. auth.', 'online news', 'press agency', 'off. auth.', 'radio/TV', 'research org.', 
'social platform', 'laboratory', 323, 309, 353, 325, 304, 326]

Notice howver that our event type nodes are still numbers. So we repeat the process for events, adding a mapping for region of events :

# Crete events mapping from a list
mapping_events_to_region = dict([(event[0], event[1].get("region")) for event in event_nodes_mappings])

# Relabel event nodes
G = nx.relabel_nodes(G, mapping_events_to_region)

# Show graph nodes after relabel
print(G.nodes)

And the result :

['int. org.', 'vet. auth.', 'online news', 'press agency', 'off. auth.', 'radio/TV', 'research org.', 
'social platform', 'laboratory','EUR', 'WPR', 'SEAR', 'EMR', 'AFR', 'AMR']

Indicators of centrality (centrality mesure)

In network analysis, indicators of centrality are really useful when we want to determine the importance of distinct nodes in a graph. In essence, these indicators are based on calculations of some sort of distance, to later assign numbers or rakings to nodes within a graph corresponding to their network postion. They reflect a unit’s prominence; in different substantive settings for instance, this may be its structural power, status, prestige, or visibility (Marsden, 2005). There are several centrality mesures in the literature of graph theory, but for the sake of brevity, I will (try to) explain three among them : Degree Centrality, Betweeness centrality, and Closeness Centrality

1. Degree Centrality

The degree centrality algorithm is the easiest centrality algorithm to calculate in graph data science, as it just considers the total number of relationships connected to a particular node. This centrality can be used to find nodes in a social network with many direct friendships and is often considered a measure of activity, e.g. Facebook. In social networks, for instance, the degree centrality can be used to find the the most “popular” individuals (nodes), as the ones with the largest number of followers or friends. The algorithm definition is given by :

2. Betweeness centrality

Betweenness centrality is a way of detecting the amount of influence a node has over the flow of information in a graph. The algorithm calculates shortest paths between all pairs of nodes in a graph. Each node receives a score, based on the number of shortest paths that pass through the node. The algorithm definition is given by :

where \(\sigma_{st}\) is the total number of shortest paths from node \(s\) to node \(t\) and \(\sigma_{st}(v)\) is the number of those paths that pass through \(v\) as long as \(v\) is not the end point

3. Closeness Centrality

A closeness measure conceives of a unit as central to the extent that it is related to other units via short geodesics:

where \(d_{ij}\) is the distance (length of the shortest path) of the shortest path between nodes i and j. Since the closiness centrality captures the average between each node and every other node in the graph, we use the normalized form of the average by multiplying \(1 / \sum_{j=1}^{N}d_{ij}\) by \(N - 1\).

Low closeness centrality means that a node is directly connected (or “just one connection away”) from most others in the network. In contrast, nodes in very peripheral locations may have high closeness centrality scores, indicating the high number of connections they need to take to connect to distant others in the network (Hansen et al., 2020)

Calculating indicators of centrality

Hopefullly, we won’t have to implement by hand the algorithms shown above. The great python package Networkx has ready-to-use implemetations of these and many other algorithms.

For each centrality measure discussed, we will compute and them in a plot. So we first define a helper function that will take two arguments : the desired centrality measure and the name of centrality label we want to show in the plot:

def generate_centrality_df(centrality_type,graph,plot_col_name):
  centrality = None
  if centrality_type == 'degree' :
    centrality = nx.degree_centrality(graph)
  elif centrality_type == 'betweenness':
    centrality = nx.betweenness_centrality(graph)
  elif centrality_type == 'closeness':
    centrality = nx.closeness_centrality(graph)
  assert centrality is not None, "Invalid/unsupported centrality type"
  df = pd.DataFrame.from_dict(centrality,orient='index',columns=[plot_col_name])
  return df

And we plot the three indicators of centrality:

# Define plot area
fig, axes = plt.subplots(nrows=1, ncols=3,figsize=(17, 5))

# Define dataframe based on graph data
degree_df_ai = generate_centrality_df('degree',Gai,'Degree centrality')
betweenness_df_ppa = generate_centrality_df('betweenness',Gai,'Betweenness')
closeness_df_ppa = generate_centrality_df('closeness',Gai,'Closeness')

# Plot centrality of all graph deaseases
degree_df_ai.sort_values('Degree centrality',ascending=False).plot(kind="bar",color='green',ax=axes[0],rot=75)
betweenness_df_ppa.sort_values('Betweenness',ascending=False).plot(kind="bar",color='blue',ax=axes[1],rot=80)
closeness_df_ppa.sort_values('Closeness',ascending=False).plot(kind="bar",color='red',ax=axes[2],rot=80)

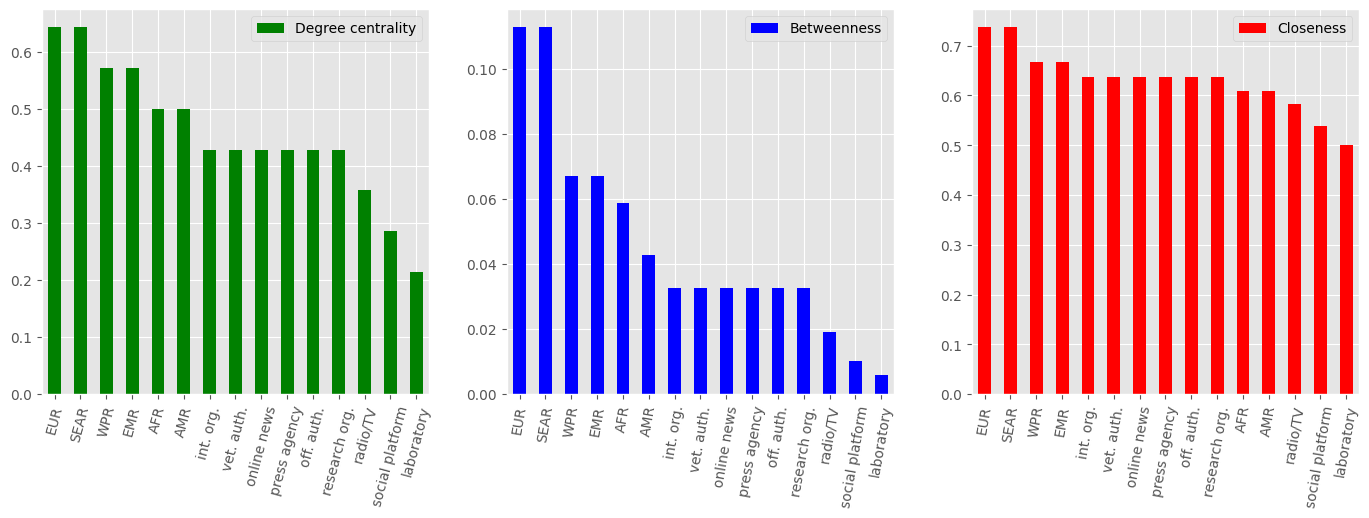
Indicators of centrality

As we can see..

Visualize graph with NzViz

fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 10))

# Define some legend parms
font = {'family': 'serif',
        'color':  'darkred',
        'weight': 'normal',
        'size': 16,
        }

# Define the circos plot
nv.circos(Gai, 
          group_by="label",node_color_by="label",node_size_by="degree",
          node_enc_kwargs={"size_scale": 0.35},edge_lw_by='count')
annotate.circos_labels(Gai, group_by="label", layout="rotate")
legend_dict = dict(ncol=1, loc='upper right', fancybox=True, shadow=True,bbox_to_anchor=(1, 1))
annotate.node_colormapping(Gai, color_by="label",legend_kwargs=legend_dict)

and the plot output :

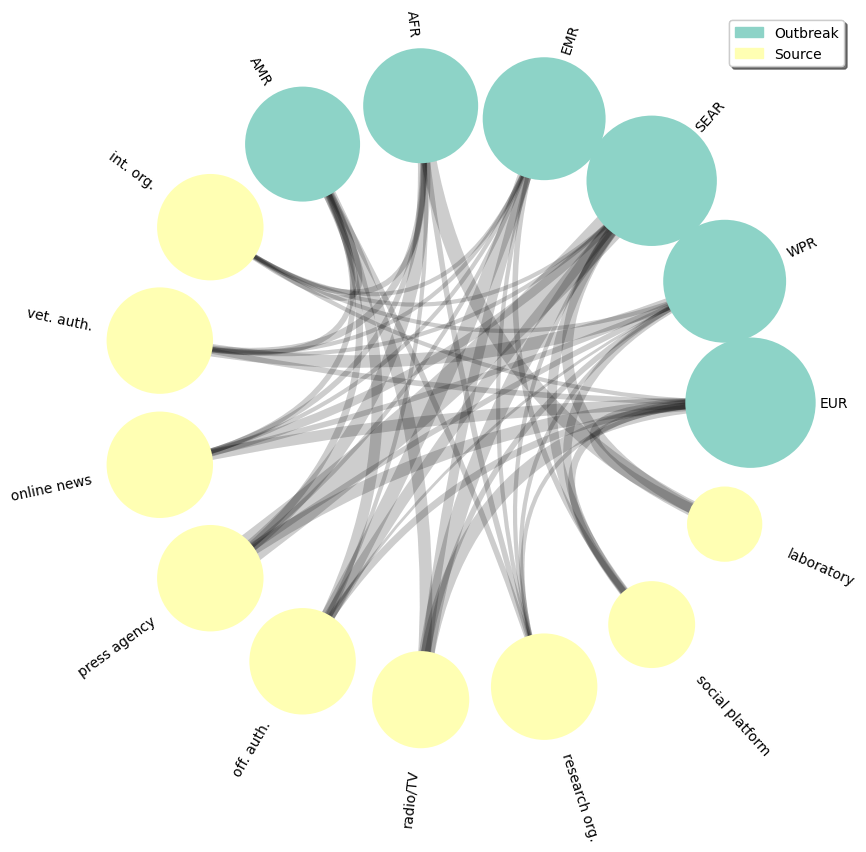
Circos plot of Avian Influenza's report events by type of reporting source and event region

Plot an interactive graphs with Pyviz

Comunity detection

Plot an interactive graph with Pyviz

References

1. Marsden, P.V., 2005. Network Analysis. Encyclopedia of Social Measurement 819–825. https://doi.org/https://doi.org/10.1016/B0-12-369398-5/00409-6

2. Reintjes, R., Zanuzdana, A., 2009. “Outbreak Investigations.” Modern Infectious Disease Epidemiology: Concepts, Methods, Mathematical Models, and Public Health. Concepts, Methods, Mathematical Models, and Public Health 159–176. https://doi.org/https://doi.org/10.1007/978-0-387-93835-6_9

3. Hansen, D.L., Shneiderman, B., Smith, M.A., Himelboim, I., 2020. Chapter 3 - Social network analysis: Measuring, mapping, and modeling collections of connections. Analyzing Social Media Networks with NodeXL (Second Edition) 31–51. https://doi.org/https://doi.org/10.1016/B978-0-12-817756-3.00003-0

4. Valentin, S., Boudoua, B., Sewalk, K., Arınık, N., Roche, M., Lancelot, R., Arsevska, E., 2024. Dissemination of information in event-based surveillance, a case study of Avian Influenza 18, e0285341. https://doi.org/https://doi.org/10.1371/journal.pone.0285341